Pengertian Limit
Limit f(x) mendekati c sama dengan L, ditulis:
}=L "\lim_{x\rightarrow c}{f(x)}=L")
jika untuk setiap x yang cukup dekat dengan c tetapi x≠c, f(x) mendekati L.
Sifat Limit Fungsi
Jika n adalah bilangan bulat positif, k konstanta, f dan g ialah fungsi-fungsi yang memiliki limit di c, maka berlaku teorema-teorema berikut.
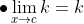
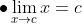
=k\lim_{x\rightarrow&space;c}f(x)\\&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}kf(x)=k\lim_{x\rightarrow c}f(x)\\ \end{align*}")
+g(x)}=\lim_{x\rightarrow&space;c}f(x)+&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}{f(x)+g(x)}=\lim_{x\rightarrow c}f(x)+ \lim_{x\rightarrow c}g(x)\\ \end{align*}")
-g(x)}=\lim_{x\rightarrow&space;c}f(x)-&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}{f(x)-g(x)}=\lim_{x\rightarrow c}f(x)- \lim_{x\rightarrow c}g(x)\\ \end{align*}")
\times&space;g(x)}=\lim_{x\rightarrow&space;c}f(x)&space;\times&space;\lim_{x\rightarrow&space;c}g(x)\\&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}{f(x)\times g(x)}=\lim_{x\rightarrow c}f(x) \times \lim_{x\rightarrow c}g(x)\\ \end{align*}")
}{g(x)}=\frac{\lim_{x\rightarrow&space;c}{}f(x)}{\lim_{x\rightarrow&space;c}g(x)}&space;\hspace{0.1cm}&space;dengan&space;\lim_{x\rightarrow&space;c}g(x)&space;\neq&space;0&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}\frac{f(x)}{g(x)}=\frac{\lim_{x\rightarrow c}{}f(x)}{\lim_{x\rightarrow c}g(x)} \hspace{0.1cm} dengan \lim_{x\rightarrow c}g(x) \neq 0 \end{align*}")
]^n=[\lim_{x\rightarrow&space;c}f(x)]^n&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}[f(x)]^n=[\lim_{x\rightarrow c}f(x)]^n \end{align*}")
}=&space;\sqrt[n]{\lim_{x\rightarrow&space;c}f(x)}&space;\hspace{0.1cm}&space;dengan&space;\lim_{x\rightarrow&space;c}f(x)&space;\geq&space;0&space;\end{align*} "\begin{align*} \bullet \lim_{x\rightarrow c}\sqrt[n]{f(x)}= \sqrt[n]{\lim_{x\rightarrow c}f(x)} \hspace{0.1cm} dengan \lim_{x\rightarrow c}f(x) \geq 0 \end{align*}")
Mencari Nilai Limit
Metode ini dilakukan dengan mensubstitusi langsung nilai kedalam fungsi f(x).
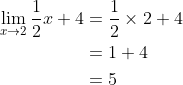
Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:
maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian bisa disubstitusikan.
(x+3)}{x-3}\\&space;&=\lim_{x\rightarrow&space;2}(x+3)\\&space;&=2+3\\&space;&=5&space;\end{align*} "\begin{align*} \lim_{x\rightarrow 2}\frac{x^2-9}{x-3}&=\lim_{x\rightarrow 2}\frac{(x-3)(x+3)}{x-3}\\ &=\lim_{x\rightarrow 2}(x+3)\\ &=2+3\\ &=5 \end{align*}")
- Metode mengalikan dengan faktor sekawan
Jika pada metode substitusi menghasilkan nilai limit yang irasional, maka fungsi dikalikan dengan akar sekawannya, kemudian bisa disubstitusikan.
(\sqrt{x}+\sqrt{7})}{x-7}\\&space;&=\lim_{x\rightarrow&space;2}(\sqrt{x}+\sqrt{7})\\&space;&=\sqrt{7}+\sqrt{7}\\&space;&=2\sqrt{7}&space;\end{align*} "\begin{align*} \lim_{x\rightarrow 2}\frac{x-7}{\sqrt{x}-\sqrt{7}} &=\lim_{x\rightarrow 2}\frac{x-7}{\sqrt{x}-\sqrt{7}} \times \frac{\sqrt{x}+\sqrt{7}}{\sqrt{x}+\sqrt{7}}\\ &=\lim_{x\rightarrow 2}\frac{(x-7)(\sqrt{x}+\sqrt{7})}{x-7}\\ &=\lim_{x\rightarrow 2}(\sqrt{x}+\sqrt{7})\\ &=\sqrt{7}+\sqrt{7}\\ &=2\sqrt{7} \end{align*}")
Limit Tak Hingga
Untuk menyelesaikan limit tak hingga dari suatu fungsi aljabar, terdapat dua cara yang umum digunakan, yaitu:
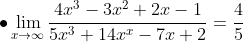
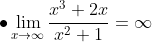
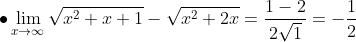
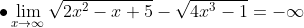
Contoh soal
Soal No.1
Carilah nilai limit berikut :
Pembahasan
c. limx→2
3x2= 3.(2)2 = 3
d. lim 3x2 + 5 = 3.(3)2 + 5 = 32x→3
e. limx→2
2x2 + 42x + 2 = 2.(22) + 42.(2) + 2 = 126 = 2
Soal No.2
Hitunglah nilai limit fungsi aljabar berikut ini:
Pembahasan
Jika hasil substitusi adalah 0/0 (bentuk tak tentu), maka tidak dapat dilakukan dengan cara memasukkan nilai langsung, melainkan harus difaktorkan terlebih dahulu
limx→2
x2 - 4x - 2 = 22 - 42 - 2 = 00 (bentuk tak tentu)
Jadi hasil faktornya adalah :
limx→2
x2 - 4x - 2 = (x-2)(x+2)(x-2) = (x+2)= (2+2) = 4
Soal No.3
Hitunglah nilai limit dibawah ini :
limx→3
x2 - 9√ x2 + 7 - 4
Pembahasan
Dengan substitusi langsung
limx→3
(x2 - 9)√ x2 + 7 - 4 = (32 - 9)√ 32 + 7 - 4 = 00
Karena diperoleh bentuk tidak tentu, maka harus digunakan cara lain yaitu menggunakan perkalian akar sekawan:
limx→3
(x2 - 9)√ x2 + 7 - 4 x √x2 + 7 + 4√ x2 + 7 + 4⇔ limx→3
(x2 - 9).(√x2 + 7 + 4)(x2 + 7) - 16 ⇔ limx→3
(x2 - 9).(√x2 + 7 + 4)(x2 - 9) ⇔ limx→3
(√x2 + 7 + 4) = (√32 + 7 + 4) = 8
Soal No.4
Hitunglah nilai limit fungsi aljabar berikut ini:
Pembahasan
Jika disubstitusi langsung, maka akan didapatkan :
limx→2
x2 - 5x + 6x2 - 4 = 22 - 5.(2) + 622 - 4 = 00 (bentuk tidak tentu)
Dengan demikian kita harus menggunakan cara lain, yaitu : dengan mengfaktorkan dan melakukan turunan. Dalam soal no.4 ini kita lakukan dengan turunan :
limx→2
x2 - 5x + 6x2 - 4 = 2x - 52x = 2.(2) - 52.(2) = -14
Soal No.5
Tentukan nilai limit dari :
Pembahasan
Perhatikan pangkat tertinggi dari x pada f (x ) = 4x – 1 dan g(x) = 2x + 1. ternyata pangkat tertinggi dari x adalah satu.
⇔ limx→∞
4xx - 1x2xx + 1x
⇔ limx→∞
4 - 1x2 + 1x
= 4 - 1∞2 + 1∞
= 4 - 02 - 0
= 2
Soal No.6
Tentukan nilai limit dari :
Pembahasan
Fungsi tersebut memiliki x dengan pangkat tertinggi 2, yaitu x2 yang terdapat pada x2 - 2. Sehingga :
⇔ limx→∞
4xx2 + 1x2x2x2 - 2x2
⇔ limx→∞
4x + 1x21 - 2x2
= 4∞ + 1(∞)21 - 2(∞)2
= 0 + 01 - 0
= 0
Soal No.7
Carilah nilai limit dari :
Pembahasan
Fungsi tersebut memiliki x dengan pangkat tertinggi 2. Sehingga :
⇔ limx→∞
2x2x2 - 5x2x2x2 - 3x2
⇔ limx→∞
2 - 5x21 - 3x2
= 2 - 5(∞)21 - 3(∞)2
= 2 - 01 - 0
= 2
Tidak ada komentar:
Posting Komentar